极大似然估计

极大似然估计来自统计学。

极大似然估计（Maximum Likelihood Estimation，MLE）是一种在统计学中用于估计概率模型参数的方法。其基本思想是：给定一组数据和一个概率模型，最大似然估计会找到模型参数的值，使得这组数据在该模型下出现的概率（即“似然性”）最大。

基本概念

似然函数（Likelihood function）是最大似然估计中的核心概念。对于给定的样本数据和某个特定的概率分布模型，似然函数是关于模型参数的函数，表示了在这些模型参数下观察到给定样本数据的概率。

定义

The most common method for estimating parameters in a parametric model is the maximum likelihood method. Let $X_1, ..., X_n$ be iid (independent and identically distributed，独立且同分布) with pdf $f (x; θ)$ .
The likelihood function is defined by
$\begin{equation} \mathcal{L}_n(\theta) = \prod_{i=1}^{n} f(X_i; \theta). \end{equation}$
The log-likelihood function is defined by
$\begin{equation} \ell_n (\theta) = \log \mathcal{L}_n(\theta). \end{equation}$
The likelihood function is just the joint density of the data, except that we treat it is a function of the parameter $\theta$ .

理解“The likelihood function is just the joint density of the data, except that we treat it is a function of the parameter $\theta$ ” 关键在于理解数据 $x$ 与参数 $\theta$ 谁是作为自变量（已知），谁是作为因变量（未知）。

一般情况下，我们是假设数据的分布符合某种固定的 pattern，也就是观察到的数据符合这个 pattern 的函数，数据未知，pattern 已知。但是似然函数反过来固定住观察到的数据，假设存在某种 pattern 使得观察的数据出现的可能性最大，因此数据已知，pattern 未知。

似然函数 $L(θ|x)$ 与观测数据 $x$ 的联合概率密度函数 $P(x|θ)$ 在数学形式上是相同的，只是自变量和因变量的角色对换了。

具体来说:

观测数据 $x$ 的联合概率密度是 $P(x|θ)$ ，以 $x$ 为自变量, $\theta$ 为因变量。
似然函数 $L(θ|x)$ 将 $\theta$ 作为自变量， $x$ 作为常数, 表示为 $\theta$ 的函数。
两者之间的关系是: $L(θ|x) = P(x|θ)$ 。

注意：

尽管数学表达式相同（即在数学上我们可以将 $L(θ|x)$ 写作等于 $P(x|θ)$ ，但它们的含义不同。 $P(x|θ)$ 表达的是数据的分布，而 $L(θ|x)$ 表达的是参数的似然度。所以，尽管它们的数学形式相同，但它们在统计推断中的角色和意义是不同的：

$P(x|θ)$ 用于描述或预测数据；
$L(θ|x)$ 用于根据已观测的数据来估计或推断参数。

步骤

最大似然估计的步骤大致如下：

定义似然函数：首先，基于模型定义似然函数。如果数据样本是独立同分布的，则似然函数是所有单个数据点概率的乘积。
对数似然：由于直接处理似然函数的乘积在数学上可能比较困难，通常会取似然函数的对数进行简化，这被称为对数似然函数。这样做的好处是乘积变成了求和，便于求导。
求导并解方程：接下来，对对数似然函数关于参数求导数，然后令导数等于零，解这些方程来找到使似然函数最大化的参数值。
求解参数：最后，求解得到的方程组，得到的参数值就是最大似然估计值。

Example

以下举两个统计学中使用 MLE 的经典例子。

抛硬币（伯努利分布）

伯努利分布(Bernoulli Distribution)是一种离散概率分布,用于描述单次试验中只有两种可能结果(成功或失败)的情况。伯努利分布由一个参数p决定,它表示单次试验中成功的概率。

数学表达式为: 若X为伯努利随机变量,则X的概率质量函数为:

$P(X=1) = p$
$P(X=0) = 1-p$

其中, $X=1$ 表示成功, $X=0$ 表示失败。

抛硬币实验是伯努利分布的一个典型例子。

假设 X1, . . . , Xn 服从伯努利分布 Bernoulli(p)。概率质量函数为 $f(x; p) = p^x (1-p)^{1-x}$ 对于 $x=0, 1$ 。未知参数是 p。那么,

似然函数为：

L_n(p) = \prod_{i=1}^n f(X_i; p) = \prod_{i=1}^n p^{X_i} (1-p)^{1-X_i} = p^S (1-p)^{n-S}

其中 $S = \sum_i X_i$ （假设为硬币正面朝上的次数，对应负面朝上的次数为 $n-S$ ）。因此,

\ell_n(p) = S \log p + (n - S) \log(1 - p)

对 $\ell_n(p)$ 求导，令其等于 0，可得最大似然估计 $\hat{p}_n = S/n$ 。

这个结果（ $\hat{p}_n = S/n$ ）直观上很有意义，表示正面朝上的概率估计就是正面出现的次数除以总的投掷次数，所以我们日常觉得习以为常就该这么算的直觉，其背后是有理论支持的。

正态分布

该示例的计算比较复杂，可跳过推导看结果。

假设我们有一个样本集 $X = {x_1, x_2, ..., x_n}$ ，我们想设计理论样本来自一个正态分布 $N(\mu, \sigma^2)$ 。其中 $\mu$ 是均值， $\sigma^2$ 是方差。我们的目标是基于样本集 $X$ ，使用MLE方法估计正态分布的参数 $\mu$ 和 $\sigma^2$ 。

定义似然函数：

对于正态分布，每个样本点 $x_i$ 的概率密度函数(PDF)为:

f(x_i|\mu,\sigma^2) = \frac{1}{\sqrt{2\pi\sigma^2}}\ \exp\left(-\frac{(x_i-\mu)^2}{2\sigma^2}\right)

由于样本是独立同分布的，整个样本集 $X$ 的似然函数就是个体样本概率密度的乘积:

L(\mu,\sigma^2|X) = \prod_{i=1}^n \frac{1}{\sqrt{2\pi\sigma^2}}\ \exp\left(-\frac{(x_i-\mu)^2}{2\sigma^2}\right)

对数似然函数

取对数两边可化简，得到对数似然函数:

\log L(\mu,\sigma^2|X) = \sum_{i=1}^n \log \frac{1}{\sqrt{2\pi\sigma^2}} - \frac{(x_i-\mu)^2}{2\sigma^2}

简化后:

\log L(\mu,\sigma^2|X) = -\frac{n}{2}\log(2\pi\sigma^2) - \frac{1}{2\sigma^2}\sum_{i=1}^n(x_i-\mu)^2

求解参数

求解 $\mu$ :

对 $\mu$ 和 $\sigma^2$ 分别求导，并令导数等于零，求解得到最大似然估计值。

\frac{\partial\log L}{\partial\mu} = \frac{1}{\sigma^2}\sum_{i=1}^n(x_i - \mu) = 0

解得:

\hat{\mu} = \frac{1}{n}\sum_{i=1}^n x_i

这表示 $\mu$ 的最大似然估计是样本的平均值。

求解 $\sigma^2$ :

\frac{\partial\log L}{\partial\sigma^2} = -\frac{n}{2\sigma^2} + \frac{1}{2(\sigma^2)^2}\sum_{i=1}^n(x_i - \mu)^2 = 0

解得:

\hat{\sigma}^2 = \frac{1}{n}\sum_{i=1}^n(x_i - \hat{\mu})^2

这表示 $\sigma^2$ 的最大似然估计是样本方差。 注意这里使用的是 $n$ 而不是 $n - 1$ ,这是因为在最大似然估计中我们不做无偏估计的修正。

逻辑回归

极大似然估计与逻辑回归有什么关系？

逻辑回归（Logistic Regression，以下简称 LR）是一种统计分析方法，用于解决二分类问题。它的目的是找到一个最佳的模型来预测目标变量的概率，目标变量的取值是离散的，通常是0和1。逻辑回归虽然名字中有“回归”二字，但它实际上是一种分类算法，主要用于处理分类任务，特别是二分类问题。

理解 LR 三要素：

LR 自身数学形式——sigmoid 函数
构建 LR 训练目标函数——极大似然估计（极大似然估计与逻辑回归的关系在这）和交叉熵
LR 训练求解参数——梯度下降

LR 自身数学形式

在逻辑回归中，我们预测的是事件发生的概率，这个概率是通过sigmoid函数来估计的。sigmoid函数可以将任意实数映射到（0,1）区间内，这样就可以将线性回归模型的输出值转化为概率。

sigmoid 表达式为：

\sigma(x)=\frac{1}{1+e^{-x}}=\frac{e^x}{1+e^x}

sigmoid 图像如下：

输入到 sigmoid 函数的 $x$ 可以理解为各种特征，然后加权求和汇总为一个值输入到 sigmoid，sigmoid 输入一个概率值。

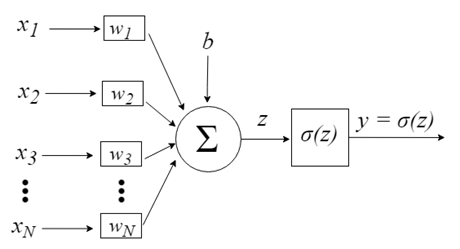
LR 推断过程：

将特征向量: $x=(x_1, x_2,...,x_n)$ 作为模型的输入；
通过为各特征赋予相应的权重 $(w_1, w_2,...,w_{n+1})$ , 来表示各特征的重要性差异，将各特征进行加权求和，得到 $x^Tw$ ；
将 $x^Tw$ 输入 sigmoid 函数，使之映射到 0~1 的区间，得到最终的概率。

综上，逻辑回归模型整个推断过程的数学形式：

f(x)=\frac{1}{1+\mathrm{e}^{-(w \cdot x+b)}}

可展开理解：

P(y=1|\mathbf{x}) = \frac{1}{1 + e^{-(b + w_1x_1 + w_2x_2 + \ldots + w_px_p)}}

我们的目标便是求解这些 $(w_1, w_2,...,w_{n+1})$ 。

构建 LR 训练目标函数

MLE

回应标题，极大似然估计与逻辑回归有什么关系？

在逻辑回归中，最大似然估计（MLE）是用来估计模型参数（即权重）的方法，使得观测到的数据在这个模型下出现的概率最大化。

逻辑回归的数学形式如上所示，这里表示成 $f_w{(x)}$ 。对于一个输入样本 $x$ , 预测结果为正样本（类别 1 ) 和负样本（类别 0 ) 的概率:：

\left\{\begin{array}{l} P(y=1 \mid x ; \boldsymbol{w})=f_{\boldsymbol{w}}(\boldsymbol{x}) \\ P(y=0 \mid \boldsymbol{x} ; \boldsymbol{w})=1-f_{\boldsymbol{w}}(\boldsymbol{x}) \end{array}\right.

综合起来，可以写成：

P(y \mid x ; \boldsymbol{w})=\left(f_w(x)\right)^y\left(1-f_w(x)\right)^{1-y}

由极大似然估计的原理可写出逻辑回归的目标函数：

L(\boldsymbol{w})=\prod_{i=1}^m P(y \mid \boldsymbol{x} ; \boldsymbol{w})

由于目标函数连乘的形式不方便计算，故在两侧取 log，并加上负号，将求最大值的问题转换成求极小值的问题，最终的目标函数形式如（详细推导过程略）：

\begin{gathered} J(w)=-\frac{1}{m} l(w)=-\frac{1}{m} L(w) \\ =-\frac{1}{m}\sum_{i=1}^m\left(y^i \log f_w\left(x^i\right)+\left(1-y^i\right) \log \left(1-f_w\left(x^i\right)\right)\right. \end{gathered}

这便是我们使用 MLE 构造出训练 LR 的 loss 函数，由于 MLE 是找到使似然函数最大化的参数值，而我们接下来使用的梯度下降的方法一般是求解该函数的最小值，所以我们在对数似然函数外面加了一个负号。

交叉熵

如果你有机器学习基础，你看上面 MLE 推导出来的目标函数（loss）有没有觉得很熟悉？这不就是二分类中的交叉熵损失函数吗？

交叉熵损失函数（Cross-Entropy Loss Function）起源于信息论，在机器学习中常用于分类问题，这是因为，如果模型的预测分布与真实分布越接近，那么它们的交叉熵就越小。因此，通过最小化交叉熵，可以优化模型的性能。

交叉熵：

H(p,q) =-\sum_{i=1}^n p(x_i)log(q(x_i))

Q：在用 MLE 推导 LR 的训练目标函数的时候，结果刚好就是交叉熵（cross entropy），这是各自不同的理论导向相同的目标函数吗？

在逻辑回归模型中，使用最大似然估计(MLE)推导出的训练目标函数，结果刚好就是交叉熵损失函数。这的确是两种不同的理论导向，却得到了相同的目标函数形式。
具体来说，在二分类问题中:
最大似然估计的角度出发，我们最大化观测数据的似然函数，也就是最大化 y=1 时概率的乘积与 y=0 时概率的乘积之积。这在上述取对数 log 后会得到一个交叉熵的形式。
从交叉熵的角度,我们希望模型预测的概率分布 q(x) 尽可能接近真实的标签分布 p(x),也就是最小化它们之间的交叉熵 H(p, q)。
经过数学推导，上述两个角度所得到的目标函数形式是完全一致的。
尽管最大似然估计和交叉熵起源于不同的理论视角，但在推导逻辑回归的优化目标时，它们殊途同归，归结为了同一个目标函数形式。这也从另一个角度印证了交叉熵在分类问题中作为损失函数的合理性和普适性。
在逻辑回归中使用 MLE 求估计参数实际上等同于最小化交叉熵损失函数。这种等价性是因为两种方法都在尝试相同的事情：使得模型的预测尽可能接近真实的数据分布。在二分类问题中，这就意味着最大化对数似然函数与最小化交叉熵损失函数是同一个事。

梯度下降训练

在得到逻辑回归的目标函数（loss 函数）后，需对每个参数求偏导，得到梯度方向，对 $J(w)$ 中的参数 $w_j$ 求偏导的结果如：

\frac{\partial}{\partial w_j} J(w)=\frac{1}{m} \sum_{i=1}^m\left(f_w\left(x^i\right)-y^i\right) x_j^i

在得到梯度之后，即可得到模型参数的更新公式：

w_j \leftarrow w_j-\gamma \frac{1}{m} \sum_{i=1}^m\left(f_w\left(\boldsymbol{x}^i\right)-y^i\right) \boldsymbol{x}_j^i

至此，完成了逻辑回归模型的更新推导。

接着只要不断迭代更新，直到目标函数收敛，此时得到的 $(w_1, w_2,...,w_{n+1})$ 便是最终我们想要的模型参数。

总结

逻辑回归可以使用 MLE 通过最大化观测数据的对数似然函数来估计模型参数。这个过程涉及到构建一个似然函数来表示给定参数时数据出现的概率，然后找到使这个概率最大化的参数值。这通常通过迭代优化算法实现，如梯度下降方法。通过这种方式，逻辑回归模型能够学习数据中的模式，从而有效地进行分类预测。

References

《all of statistics》
GPT4（有些细节可能有误，请注意判别）
Claude3（有些细节可能有误，请注意判别）

欢迎关注微信公众号👏 code

欢迎微信扫码加入我的付费知识星球👏 code